Tentang Binary Tree

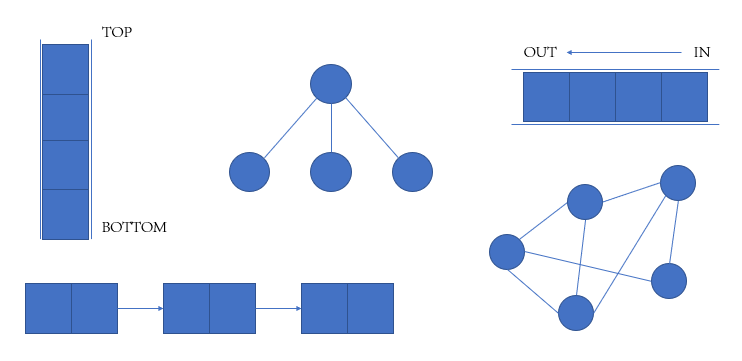
Kalau kemarin struktur data tree, kali ini kita akan bahas tentang bentuk tree yang lebih spesifik yaitu binary tree.

Untuk mengingat kembali tentang apa itu tree, silahkan kunjungi alamat berikut Tentang Struktur Data Tree – Antek Teknologi.

 

Pengertian

---

Binary tree adalah sebuah tree yang setiap node-nya hanya dapat memiliki maksimal 2 buah child node.

Berbeda dengan tree ‘default’ yang setiap node-nya bisa memiliki child node sebanyak apapun.

Karena tiap node hanya boleh memiliki 2 child node, maka dari itu tree yang satu ini mengambil kata binary sebagai namanya.

Seperti yang kita tahu, binary atau biner adalah sistem bilangan yang hanya mengakui dua angka saja, yaitu 0 dan 1.

Mungkin itu sedikit tentang asal-usul nama binary tree.

Kemudian tree yang satu ini umumnya digunakan untuk menyimpan banyaknya data secara terurut.

Kita akan bahas konsep pengurutan ini pada bagian berikutnya.

Jadi konsep penempatan data secara terurut ini adalah salah satu konsep yang populer diterapkan pada binary tree.

 

Konsep Binary Tree

---

Sebenarnya tree yang satu ini tidak memiliki perbedaan terlalu banyak dengan tree ‘default‘.

Istilah seperti root, node, edge, leaf, parent dan sebagainya masih berlaku juga pada pohon biner ini.

Namun sesuai dengan penjelasan sebelumnya, tiap node hanya boleh memiliki maksimal dua buah child node.

Jika contohnya node A sudah memiliki dua buah child, maka node yang baru datang tidak boleh menjadi child dari node A itu tadi.

Tetapi masih bisa menjadi keturunan dari node A dengan cara menjadi child dari node yang merupakan child dari node A.

Jadi binary tree tidak cocok untuk merepresentasikan sebuah hirarki seperti silsilah keluarga atau jabatan dan semacamnya.

Karena pasti ada kemungkinan seseorang memiliki lebih dari 2 anak.

 

Sorting Pada Binary Tree

Jenis tree yang satu ini cocok untuk menerapkan konsep sorting atau pengurutan data.

Misalkan kita memiliki himpunan data yang merupakan kumpulan angka, di antaranya, 8, 17, 3, 5, 6, 10, 2.

Dengan binary tree, kita bisa menerapkan percabangan untuk menentukan posisi setiap node sesuai dengan nilai yang ada di dalamnya.

Hasil percabangan akan sesuai dengan angka mana yang lebih kecil atau lebih besar, mari langsung saja kita coba agar tidak bingung.

Dalam contoh kali ini, kita akan menaruh node dengan angka yang lebih besar atau sama dengan untuk bergerak ke child node kanan.

Namun untuk node dengan angka yang lebih kecil, akan bergerak ke child node kiri.

Node pertama dengan nilai 8 datang dan akan langsung menjadi root node.

Kemudian node dengan nilai 17 datang, dan kita akan lakukan perbandingan dengan node dengan angka 8.

Karena 17 yang lebih besar, maka node ini akan bergerak ke kanan.

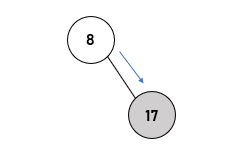
Lalu node dengan angka 3 datang, karena lebih kecil dari 8, maka akan menjadi left child node dari node 8.

Lanjut ke node dengan angka 5, karena ia lebih kecil dari 8, maka ia akan bergerak ke sebelah kiri.

Tetapi karena node 8 sudah memiliki left child node, maka node 5 harus mencari tempat lain.

Karena tadi left child node dari node 8 adalah node 3, maka sekarang 5 akan dibandingkan dengan 3.

Node 5 lebih besar daripada yang bernilai 3, maka node 5 akan bergerak ke kanan dan menjadi right child node dari node 3.

Mesikpun node 5 tidak menjadi child dari node 8, tapi node 5 tetap menjadi keturunan atau descendant dari node 8.

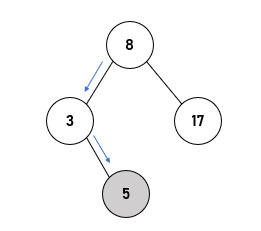
Dan berikut ini adalah beberapa gambar bagaimana binary tree tersebut terbentuk sampai dengan kedatangan node dengan angka 2.

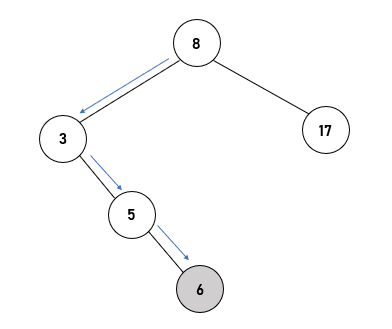
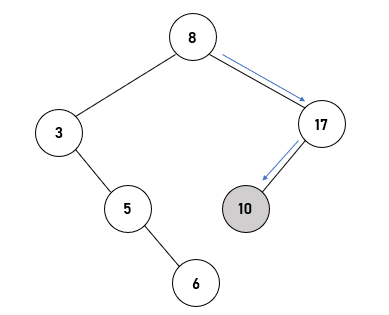
Jadi sekian untuk konsep dari binary tree yang berkaitan dengan proses pengurutan data atau sorting.

 

Jenis Binary Tree

---

Struktur data ini terbagi lagi menjadi beberapa jenis, tergantung dari posisi tiap node yang akan membentuk pola tertentu.

a. Full Binary Tree

Tree yang setiap node-nya memiliki dua buah child node, kecuali leaf node.

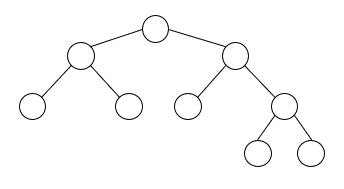
b. Completed Binary Tree

Jenis yang satu ini memiliki beberapa ketentuan.

Ketentuan pertama, setiap level yang ada harus memiliki node yang lengkap, kecuali level terakhir atau terbawah.

Ketentuan kedua, jika level terbawah memiliki node tetapi tidak lengkap, maka node yang ada harus mengisi sisi kiri dahulu baru ke kanan.

c. Perfect Binary Tree

Tree yang setiap node-nya memiliki dua buah child node, kecuali leaf node.

Namun setiap leaf node harus berada di level yang sama.

d. Balanced Binary Tree

Jika sebuah node memiliki subtree, maka selisih height untuk subtree kanan dan kiri dari node tersebut bernilai maksimal 1.

Namun jika ada satu node saja yang selisih height dari subtree kanan dan kirinya melebihi 1, maka tree ini tidak bisa disebut balanced.

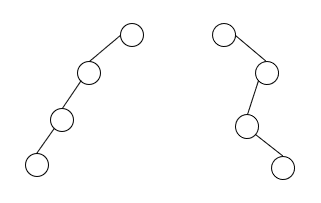
Untuk menentukan kenapa dua tree tersebut ada yang balanced dan unbalanced, mari kita fokus ke node root atau node dengan huruf R.

Baik tree yang pertama dan yang kedua, node root sama-sama memiliki dua buah subtree, subtree kanan dan yang kiri.

Untuk tree yang pertama, selisih height antara subtree kanan dan kirinya untuk root node hanya 1, subtree yang kiri height-nya 3, sedangkan yang kanan adalah 2.

Namun untuk tree yang kedua, nilai dari selisih height-nya melebihi 1 atau lebih tepatnya bernilai 2.

Karena height dari subtree kiri adalah 3, sedangkan height dari subtree kanan hanya 1.

Maka dari itu, tree yang pertama akan dianggap balanced, sedangkan yang kedua tidak atau unbalanced.

e. Skewed Binary Tree

Binary tree yang setiap node-nya memiliki tepat satu child node saja, kecuali leaf node.

 

Tree Traversal

---

Tree traversal adalah sebuah konsep bagaimana kita mengakses setiap node yang ada pada sebuah binary tree.

Jadi ada tiga buah jenis traversal, yaitu preorder, inorder dan postorder.

Sebelumnya sudah dijelaskan bahwa setiap node pada binary tree bisa memiliki maksimal dua buah child node.

Child-nya bisa berada di sebelah kiri atau left child node dan bisa di sebelah kanan atau right child node.

Karena ada left dan right child node ini, kita bisa menerapkan sebuah konsep yang namanya tree traversal dengan lebih teratur.

Jadi ada 3 pilihan, akses data di dalam node, pindah ke left child node dan pindah ke right child node.

Dan ketiga jenis tree traversal ini sebenarnya hanya menaruh bagian “akses data di dalam node” di 3 tempat yang berbeda.

a. Preorder

Akses data di dalam node -> Pindah ke left child node -> Pindah ke right child node.

b. Inorder

Pindah ke left child node -> Akses data di dalam node -> Pindah ke right child node.

Sekedar info, inorder traversal adalah traversal yang bisa menampilkan data secara terurut sesuai dengan penempatan node.

c. Postorder

Pindah ke left child node -> Pindah ke right child node -> Akses data di dalam node.

Kalau masih belum paham, silahkan lihat dan simak gambar di bawah ini.

Berdasarkan gambar di atas, kita akan coba menampilkan setiap data di dalam node menggunakan ketiga tree traversal tadi.

Dan berikut ini adalah hasil dari sebuah program sederhana yang menampilkan hasil dari ketiga tree traversal tadi sesuai dengan binary tree di atas.

 

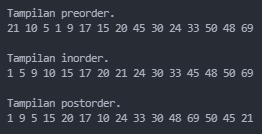
Rangkuman

---

Jadi struktur data binary tree merupakan salah satu jenis atau mungkin satu-satunya jenis dari struktur data tree.

Struktur data ini hanya memperbolehkan setiap node memiliki maksimal dua buah child node dan cocok untuk menyimpan data secara terurut.

Kemudian ada banyak istilah dan berbagai jenis yang bisa kalian temukan saat mempelajari binary tree.

Untuk istilah-istilah yang berlaku, secara garis besar sama dengan yang berlaku pada struktur data tree “default“.

Dan terakhir, ada 3 jenis tree traversal yang umum diterapkan pada struktur data ini, yaitu preorder, inorder dan postorder.

Sekian untuk artikel ini, terima kasih.