Implementasi Struktur Data Graf Dalam Algoritma Routing

Di era teknologi saat ini, jaringan komputer sudah sangat umum digunakan dalam berbagai aspek kehidupan masyarakat.

Jaringan komputer terdiri dari sejumlah komputer yang terhubung satu sama lain melalui saluran komunikasi seperti kabel, gelombang mikro, dan gelombang radio.

Jaringan komputer dapat digambarkan atau dimodelkan dengan menggunakan graf.

Artikel ini membahas tentang salah satu penerapan teori graf dalam kehidupan sehari-hari, yaitu penerapan algoritma Dijkstra yang merupakan bagian teori dalam struktur data graf.

Pada bagian awal dijabarkan secara ringkas beberapa definisi dan sejarah graf.

Bagian selanjutnya adalah pembahasan mengenai algoritma Dijkstra dan fungsi router.

Untuk penerapan algoritma Dijkstra disini digunakan untuk menyelesaikan permasalahan routing pada jaringan komputer.

 

Definisi Graf

Dalam struktur data, graf merupakan data struktur non-linear yang terdiri dari simpul (vertex atau yang akan lebih sering disebut node  pada artikel ini ) dan sisi (edge). Suatu node dapat terhubung dengan node lain atau dirinya sendiri dengan menggunakan edge. Edge disini melambangkan hubungan yang terjadi di kedua ujung edge.  Kumpulan  node yang dihubungkan dengan edge akan membentuk graf.

Node dalam struktur data ini dapat berupa sebuah entitas atau perwujudan dari suatu benda. Tiap node akan memiliki identitasnya sendiri sesuai kebutuhan. Hubungan yang terjadi diantara node tersebut dapat merepresentasikan berbagai masalah dalam kehidupan nyata, sebagai contohnya hubungan pertemanan dari node pengguna, hubungan jaringan dari node komputer, rute jalan dari node tempat dan masih banyak lagi [1]. Dari representasi tersebut, terdapat banyak masalah yang dapat dimodelkan dan dipecahkan menggunakan teori graf.

 

Sejarah Graf

Sebagai salah satu cabang dari matematika, teori graf memiliki sejarah yang panjang. Sejarah dari teori ini dapat ditelusuri hingga tahun 1735, dimana pada saat itu terdapat matematikawan Swiss bernama Leonhard Euler yang berhasil memecahkan permasalahan “Königsberg bridge” atau jembatan Königsberg.  Permasalahan ini merupakan sebuah puzzle lama untuk mengetahui kemungkinan mencari rute untuk melintasi 7 buah jembatan yang merentang pada sebuah sungai bercabang dua yang melintasi sebuah pulau dengan batasan tanpa melewati jembatan lebih dari sekali.

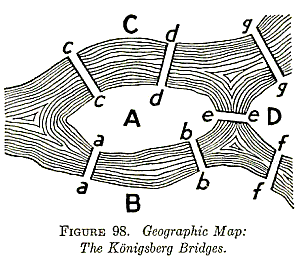
Menurut Euler, tidak ada rute yang dapat memenuhi syarat tersebut. Euler membuktikan teorinya dengan memberikan referensi pada penempatan jembatan secara fisik. Teori ini kemudian nantinya akan dikenal sebagai teori pertama pada teori graf yaitu teori rute Euler [2].

 

Fungsi Router

Router merupakan sebuah perangkat jaringan yang bertugas untuk melakukan routing yaitu menghubungkan antara jaringan satu dengan jaringan yang lain [3]. Router mengidentifikasi setiap jaringan berdasarkan sebuah alamat unik yang dikenal dengan nama IP (Internet Protocol).

Setiap router pada sebuah jaringan lokal akan menghubungkan perangkat-perangkat yang ada pada jaringan tersebut ke jaringan lokal yang lain. Adanya interaksi antar jaringan ini akan terus bertambah seiring dengan bertambahnya jaringan lokal lain yang terhubung. Kumpulan dari jaringan-jaringan lokal yang saling terhubung dan membentuk sebuah jaringan global dan berskala besar selanjutnya dikenal dengan istilah Internet.

 

Graf untuk Menyelesaikan Permasalahan Routing

Permasalahan utama dalam kasus routing ini adalah bagaimana cara agar paket data dikirimkan ke komputer tujuan melewati hop-hop yang dapat berupa sebuah router di internet dengan beban (cost) seminimum mungkin. Beban pada kasus ini adalah besarnya latency data. Latency merupakan lamanya waktu yang diperlukan sebuah data untuk berpindah dari satu titik ke titik lainnya, dimana setiap titik merupakan sebuah router untuk jaringan yang berbeda. Latency dihitung dengan satuan milidetik. Solusi dari permasalahan ini adalah informasi mengenai waktu tercepat dari paket data untuk sampai ke tujuan.

Kasus di atas akan diselesaikan dengan metode penyelesaian shortest path problem pada graf. Shortest path problem merupakan salah satu permasalahan graf berbobot untuk menentukan jarak terpendek dari satu node ke node tujuan. Algoritma djikstra dapat diterapkan untuk menyelesaikan shortest path problem [4].

 

Algoritma Djikstra

Ketika ingin berpergian ke suatu tempat, seperti mall, rumah sakit, sekolah, kantor, dan lain-lain, tentunya setiap orang akan memilih rute atau jalur terpendek untuk dilalui guna mempersingkat waktu perjalanan dari tempat asal ke tempat tujuan. Dalam graph sendiri, tempat asal dan tujuan dianalogikan sebagai simpul/vertex sedangkan rute/jalur/lintasannya dianalogikan sebagai edge.

Algoritma Dijkstra adalah salah satu algoritma /urutan langkah yang digunakan dalam melakukan pemecahan masalah graph baik berarah (directed graph) maupun tidak berarah (undirected graph) [4]. Permasalahan graph yang dapat diselesaikan menggunakan algoritma ini yaitu permasalahan dalam pencarian rute atau jalur terpendek (shortest path) dalam suatu graph berbobot.

Penggunaan algoritma Dijkstra dalam optimalisasi penentuan jalur terpendek ini pertama kali ditemukan oleh seorang ilmuan bernama Edger Wybe Dijkstra yang dimana beliau mencoba menyelesaikan permasalahan pencarian minimum cost dari suatu vertex x ke vertex y dalam graph berbobot dengan nilai bilangan positif.
Penerapan dari algoritma jenis ini diawali dengan menentukan suatu titik/vertex yang menjadi tujuan awal/asal yang kemudian diberikan nilai atau bobot jarak dari titik asal ke titik terdekat selanjutnya secara bertahap yang kemudian akan dilakukan pengembangan dalam pencarian titik-titik berikutnya.

Adapun tahapan algoritmanya adalah sebagai berikut:
1) Menentukan vertek atau titik awal dan beri bobot pada vertek/titik terdekat. Algoritma ini akan melakukan penelusuran path pada setiap vertex.
2) Beri nilai 0 pada vertex awal dan nilai tak hingga (0) terhadap vertek/titik lain yang belum terisi. Set vertex awal sebagai posisi awal.
3) Pada posisi awal, pilihlah vertex yang memiliki bobot terkecil pada vertek/titik tetangganya. Hapus jika nilai bobot lebih kecil dari nilai sebelumnya dan update yang memiliki bobot baru.
4) Tandai vertex yang telah dilalui sebagai vertex dilewati, jarak yang disimpan adalah jarak terakhir dan yang paling minimal bobotnya.
5) Set vertex yang belum dilewati dengan jarak terkecil (dari vertex keberangkatan) sebagai vertex keberangkatan dan selanjutnya ulangi langkah-langkah sebelumnya sampai dengan vertek/titik tujuan dikunjungi.

Adapun penerapan algoritma djikstra menggunakan bahasa C adalah sebagai berikut:

#include 
#include 
#include 
#define MAX 10
#define MAX_WEIGHT 999

void background();
void dijkstra(int graf[MAX][MAX], int n, int x);

int main(){
    int nVertex, start, end, i, j, value;
    int graf[MAX][MAX];
    background();
    printf("Input Jumlah Verteks\t: ");
    scanf("%d", &nVertex);
    
    printf("\n");
    for(i = 0; i < nVertex; i++){
        for(j = i + 1; j < nVertex; j++){
            if(i != j){
                printf("Input bobot verteks %d dengan verteks %d (Input nilai 0 jika tidak terhubung)\t: ", i + 1, j + 1);
                scanf("%d", &value);
                graf[i][j] = graf[j][i] = value;
            }   
        }
    }

    for(i = 0; i < nVertex; i++){
        graf[i][i] = 0;
    }

    puts("\nMatriks Ketetanggaan\n");
    for(i = 0; i < nVertex; i++){
        for(j = 0; j < nVertex; j++)
            printf("%d\t", graf[i][j]);
        printf("\n");
    }

    printf("\nInput verteks awal\t: ");
    scanf("%d", &start);
    while(i){
        if(start < 1 || start > nVertex )
            puts("Verteks tidak ada");
        else
            i = 0;
    }

    dijkstra(graf, nVertex, start);

    return 0;
}

void background(){
    system("cls");
    puts("\t\tPROGRAM IMPLEMENTASI ALGORITMA DJIKSTRA\n");
}

void dijkstra(int graf[MAX][MAX], int n, int x){
    int weight[MAX][MAX], visited[MAX], distance[MAX];
    int minimum, i, j, nextNode, count, awal = x - 1, tujuan;

    for(i = 0; i < n; i++){
        for(j = 0; j < n; j++){
            if(i == j)
                weight[i][j] = 0;
            else{
                if (graf[i][j] == 0)
                    weight[i][j] = MAX_WEIGHT;
                else
                    weight[i][j] = graf[i][j];
            }
        }
    }

    for(i = 0; i < n; i++){
        distance[i] = weight[awal][i];
        visited[i] = 0;
    }

    distance[awal] = 0;
    visited[awal] = 1;
    count = 1;

    while(count < n - 1) {
        minimum = MAX_WEIGHT;
        for(i = 0; i < n; i++){
            if(distance[i] < minimum && !visited[i]){
                minimum = distance[i];
                nextNode = i;
            }
        }

        visited[nextNode] = 1;
        for(i = 0; i < n; i++){
            if(!visited[i]){
                if(minimum + weight[nextNode][i] < distance[i])
                    distance[i] = minimum + weight[nextNode][i];
            }
        }
        count++;
    }

    printf("Input verteks tujuan\t: ");
    scanf("%d", &tujuan);
    printf("Bobot jarak terpendek dari verteks %d ke verteks %d adalah %d\n", awal + 1, tujuan, distance[tujuan - 1]);
}

 

Penjelasan Program

Karena program ini menggunakan bahasa pemrograman C, maka seperti biasa program ini akan diawali dengan pemanggilan beberapa file header. Kemudian ada deklarasai sekaligus inisialisasi konstanta MAX dan MAX_WEIGHT serta dua buah fungsi yaitu fungsi background() dan fungsi dijkstra beserta beberapa parameternya. Kemudian kita masuk ke fungsi utama atau fungsi main, awalnya pengguna akan diminta untuk memasukkan nilai dari jumlah verteks dahulu.

Setelah itu pengguna akan diminta lagi untuk memasukkan nilai dari edge antar verteks. Untuk verteks dengan angka yang sama, nilai atau bobot dari edge-nya akan diberikan nilai 0. Lalu akan ada perulangan yang akan menampilkan tampilan visual dari matriks ketetanggaan yang sesuai dengan input dari pengguna. Setelah itu pengguna akan diminta lagi untuk memasukkan angka yang akan mewakili verteks awal, selanjutnya program akan masuk ke fungsi dijkstra dengan parameter yaitu array graf, variabel nVertex dan variabel start.

Kita berlanjut ke fungsi dijkstra, fungsi ini awalnya akan memberikan nilai 0 kepada setiap verteks yang memiliki nilai 0, jadi nilai 0 itu dirubah menjadi 0. Kemudian ada perulangan yang digunakan untuk memasukkan nilai ke dalam array distance dan array visited. Array distance sendiri akan mencatat beberapa nilai bobot sedangkan array visited akan menjadi penanda apakah sebuah verteks sudah dikunjungi atau belum. Setelah itu kita akan beralih ke perulangan while yang di dalamnya terdapat dua buah perulangan for.

Fungsi dari perulangan for pertama adalah untuk mencari edge terpendek yang dekat dengan verteks tujuan serta memindahkan variabel nextNode ke verteks yang terhubung dengan edge tersebut. Dan perulangan for kedua bertugas untuk menjumlahkan edge dari tiap verteks awal sampai dengan tujuan. Hasil dari kedua perulangan for itu adalah sebuah array distance yang sudah berisi nilai dari jalur terpendek antara verteks awal dengan masing-masing verteks tujuan. Kemudian di saat pengguna memasukkan input verteks tujuan, program hanya akan menyesuaikan indeks verteks tujuan dengan indeks yang ada di array distance dan mencetak output akhir.

 

Contoh Kasus

Pak Herman ingin mendownload video dari situs facebook. Setelah komputer Pak Herman meminta file ke server facebook barulah file-file tersebut akan dikirimkan dari server facebook melewati router-router yang ada di Internet untuk sampai ke komputer Pak Herman. Terdapat suatu waktu ketika data ingin dikirimkan dari server keadaan di Internet memiliki kondisi jaringan seperti gambar berikut.

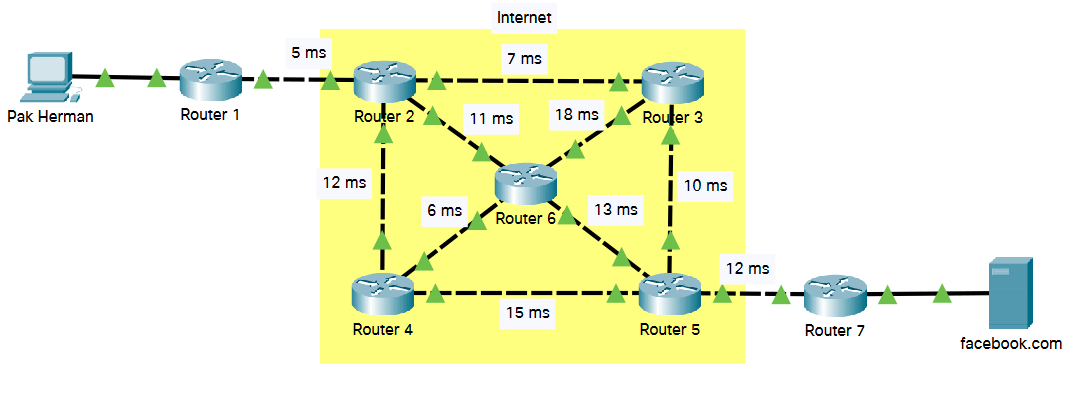
Tentukan berapakah waktu tercepat yang dibutuhkan untuk paket tersebut dikirimkan dari server facebook ke komputer Pak Herman.

 

Penyelesaian

Terlebih dahulu permasalahan akan direpresentasikan ke dalam bentuk graf berbobot. Setiap router akan disimbolkan sebagai sebuah node pada graph, hubungan antar router disimbolkan sebagai edge, dan besarnya latency akan menjadi bobot dari setiap edge. Berikut merupakan hasil dari representasi permasalahan tersebut ke dalam graf:

Tahap selanjutnya adalah merepresentasikan graf tersebut ke dalam sebuah matriks dua dimensi untuk mempermudah penyelesaiannya dalam program nantinya. Representasi graf tersebut dalam matriks adalah sebagai berikut:

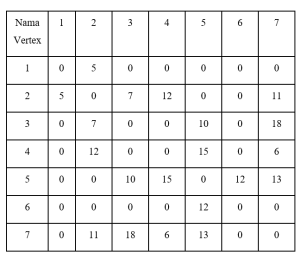
Tahap terakhir adalah memasukkan matriks ke dalam program algoritma djikstra.

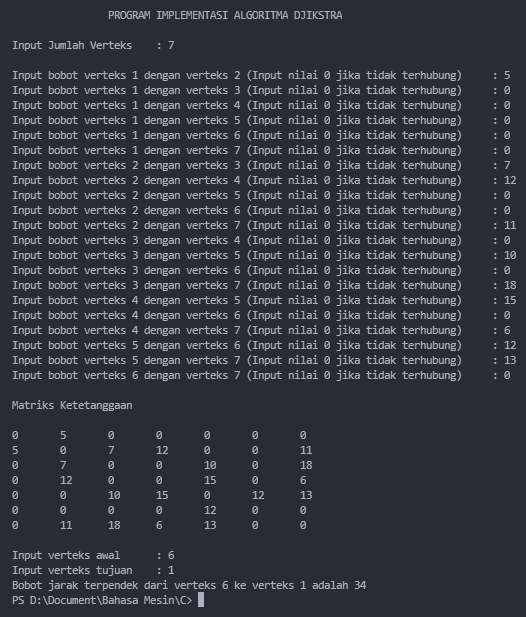
Dengan demikian didapat penyelesaian bahwa, waktu tercepat yang diperlukan agar paket dapat dikirimkan dari server facebook ke komputer Pak Herman adalah sebesar 34 milidetik.

 

Kesimpulan

Berdasarkan penjelasan di atas, dapat kita simpulkan bahwa teori struktur data graf sangat berguna dalam kehidupan sehari-hari dan dapat diimplementasikan terutama dalam menyelesaikan masalah routing pada jaringan komputer. Jaringan komputer dapat digambarkan/dimodelkan dengan menggunakan graf. Salah satu algoritma yang dapat digunakan untuk menyelesaikan masalah routing pada jaringan komputer adalah algoritma Dijkstra. Maka dari itu, teori graf dan teori-teori struktur data lainnya sangat penting digunakan untuk mengembangkan ilmu pengetahuan sehingga dapat membantu kehidupan masyarakat.

 

Daftar Pustaka

[1] S. Carlson, “graph theory,” 24 November 2020. [Online]. Available: https://www.britannica.com/topic/graph-theory.
[2] E. W. Weisstein, “Königsberg Bridge Problem,” 9 Desember 2020. [Online]. Available: https://mathworld.wolfram.com/KoenigsbergBridgeProblem.html.
[3] T. McMillan, Cisco Networking Essential, Indianapolis, : John Wiley & Sons, Inc, 2012.
[4] V. V. Dus, Principle of Data Stuctures Using C and C++, India: New Age International, 2006.

 

Identitas Penulis

Kelompok E2 Kelas E:

(2008561030) Hans Rio Alfredo Palla

(2008561040) I Komang Surya Adinandika

(2008561045) I Made Alit Darma Putra

(2008561050) Gusti Ngurah Deva Wirandana Putra

(2008561055) I Made Juniandika

 

Program Studi Informatika

Fakultas Matematika dan Ilmu Pengetahuan Alam

Universitas Udayana

2021