Bilangan Desimal dan Konversi Desimal

Artikel kali ini akan membahas sedikit dari bilangan desimal dan lumayan banyak materi tentang konversi dari bilangan desimal.

Namun bilangan desimal yang akan kita bahas bukanlah bilangan atau angka yang berada di belakang koma atau titik itu ya, tapi sistem bilangan desimal.

Mari langsung saja kita ke pembahasan.

 

Bilangan Desimal

---

Bilangan desimal yang akan kita bahas pada kesempatan kali ini bukanlah bilangan desimal yang kita bayangkan seperti 3.14 atau 2.71 serta bilangan yang tidak bulat lainnya.

Sistem bilangan desimal ini adalah sistem bilangan yang umumnya digunakan sehari-hari oleh manusia.

Contohnya angka yang muncul pada barang-barang buatan manusia seperti tombol angka pada papan ketik ponsel komputer atau remote televisi.

Sistem bilangan ini mengakui 10 karaker angka atau berbasis 10, yaitu 0, 1, 2, 3, 4, 5, 6, 7, 8 dan 9.

Berbeda dengan bilangan biner, bilangan desimal tetap dibaca dari kiri ke kanan.

Contoh dari bilangan desimal adalah 179₁₀.

Angka 10 yang tertulis dengan ukuran kecil itu menandakan basis atau tipe dari bilangan ini, yaitu sistem bilangan desimal.

Penulisan basis itu sendiri tidak wajib ada, karena hanya untuk memperjelas saja.

Misalkan contohnya dengan angka 10.

Angka 10 ini bisa saja adalah bilangan biner atau desimal, dan basis bisa kita pakai untuk mencegah kebingungan yang mungkin terjadi.

Baik itu tadi tentang sistem bilangan desimal, sekarang kita akan membahas tentang konversi bilangan desimal ke sistem bilangan yang lain.

 

Konversi Bilangan Desimal

---

Cara mengkonversikan bilangan desimal ke dalam bentuk biner, oktal maupun heksadesimal memiliki cara yang serupa tapi tak sama.

Sederhananya, kalian hanya cukup membagi bilangan desimal tersebut dengan angka yang merupakan basis dari sistem bilangan yang menjadi tujuan konversi.

Jika ingin mengubahnya ke bentuk biner, maka bilangan desimalnya akan terus masuk ke pembagian 2.

Kalau oktal pembagian 8 dan heksadesimal pembagian 16.

Pembagian ini akan terus berlanjut sampai hasil pembagian sudah kurang dari 1.

Proses pembagian yang diterapkan juga bukanlah jenis pembagian biasa yang sering kita temui, melainkan operasi matematika modulus.

Operasi modulus sendiri akan menghasilkan nilai yang merupakan sisa dari hasil pembagian yang ada.

Nilai dari sisa pembagian inilah yang nantinya akan terus kita catat sampai setiap terjadinya operasi modulus ini.

Baik itu saja untuk pendahuluannya, sekarang kita berlanjut ke konversi untuk masing-masing sistem bilangan seperti biner, oktal dan heksadesimal.

 

Konversi Desimal ke Biner

Sesuai dengan penjelasan sebelumnya, kita akan membagi bilangan desimal dengan jumlah basis angka dari sistem bilangan yang merupakan tujuan konversi.

Kali ini kita akan mencoba mengkonversikan bilangan desimal ke bentuk biner, sistem bilangan yang hanya mengakui dua karakter saja, yaitu 0 dan 1.

Baca juga : Bilangan Biner dan Konversi Biner – Antek Teknologi

Karena hanya berbasis dua angka, maka kita akan membagi bilangan desimal dengan angka 2 secara terus menerus sampai hasilnya menyentuh angka 0.

Jika hasil pembagian menghasilkan nilai yang tidak bulat, maka kita bulatkan nilai tersebut ke bawah.

Contoh, angka 1.3 menjadi 1.

Selama melakukan pembagian, kita akan mencatat setiap sisa yang dari setiap hasil pembagian.

Mari kita coba, misalkan bilangan desimalnya adalah 30.

• Pertama, kita bagi 30 dengan 2, dapat hasil 15 dengan sisa tidak ada atau 0.
• Kita catat sisanya dan hasil pembagian kita bagi dengan 2 lagi.
• Lanjut 15 bagi 2 dapat hasil 7 yang merupakan pembulatan dari 7.5 dan sisa dari pembagian adalah 1.
• Sekedar info, kalian bisa menggunakan kalkulator modulus untuk mencari nilai dari sisa sebuah pembagian.
• Kemudian kita lanjut membagi 7 dengan 2, dapat hasil 3 yang merupakan pembulatan dari 3.5, serta sisa pembagian adalah 1.
• Lalu 3 bagi 2, dapat hasil 1.5 dibulatkan menjadi 1 dengan sisa pembagian yang didapat yaitu 1.
• Terakhir, 1 kita bagi dengan 2 dan dapat hasil 0.5, nilai 0.5 dibulatkan dapat hasil 0.
• Karena sudah menyentuh angka 0, maka pembagian sudah selesai dan sisa akan dicatat dengan nilai 1.
• Sejauh ini kita sudah mengumpulkan 5 sisa pembagian.

Tabel atau gambar di bawah menunjukkan proses pembagian yang sudah kita lakukan tadi.

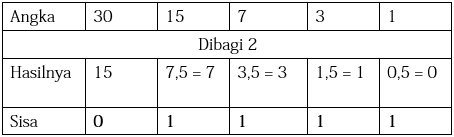
Kemudian langkah penutup, kita urutkan semua nilai sisa yang sudah tercatat tadi dengan posisi paling kanan adalah nilai sisa pembagian pertama.

Maka hasil akhir adalah 30₁₀ = 11110₂.

 

Konversi Desimal ke Oktal

Masih dengan cara yang sama dalam mengubah bentuk desimal menjadi bentuk biner.

Namun karena oktal berbasis 8 buah angka, maka kita akan membagi bilangan desimalnya dengan 8.

Baca juga : Bilangan Oktal dan Konversi Oktal – Antek Teknologi

Mari kita coba dengan contoh bilangan desimalnya 99.

• Pertama-tama kita bagi 99 dengan 8, maka hasilnya adalah 12 yang merupakan pembulatan dari 12.3.
• Kemudian kita catat sisa pembagian yaitu 3, nilai 3 ini bukan bilangan yang ada di belakang koma tapi hasil dari 99 – (8 x 12).
• 99 adalah bilangan desimal yang dibagi, 8 adalah bilangan pembagi dan 12 adalah hasil bagi yang sudah dibulatkan.
• Kemudian 12 kita bagi lagi dengan 8, dapat nilai 1 yang merupakan hasil pembulatan dari 1.5, sisa pembagian adalah 4.
• Lanjut lagi 4 bagi 8 sama dengan 0.5, karena sudah sampai 0 dan terdapat sisa, kita catat sisanya adalah 1.
• Pembulatan tidak perlu dilakukan lagi.

Berikut ini adalah gambar proses pembagian, bacanya dari kiri ke kanan.

Sesudah proses pembagian berulang selesai, kita susun nilai dari semua sisa yang sudah tercatat dari kanan ke ke kiri.

Maka hasil akhir 99₁₀ = 143₈.

 

Konversi Desimal ke Heksadesimal

Bilangan biner dan oktal sudah, sekarang kita coba mengubah bentuk desimal ke bentuk heksadesimal.

Masih dengan cara yang sama, yaitu membagi bilangan desimal dengan basis dari sistem bilangan tujuan sampai menyentuh hasil 0 dan mencatat sisa tiap pembagian yang terjadi.

Baca juga : Bilangan Heksadesimal dan Konversi Heksadesimal – Antek Teknologi

Ingatlah kalau ini adalah bilangan heksadesimal, jadi sisa pembagian di antara 10 dan 15 akan kita ubah menjadi karakter huruf.

Langsung saja kita coba dengan contoh bilangan desimalnya 435.

• Seperti biasa, 435 akan kita bagi dengan 16 yang merupakan basis dari heksadesimal, dapat 27 yang merupakan hasil pembulatan dari 27.1, kemudian sisa pembagian adalah 3.
• Sekedar info, kalau bingung mencari nilai dari sisa, kalian bisa menggunakan kalkulator modulus.
• Kemudian 27 bagi 16 dapat hasil yang sudah dibulatkan yaitu 1 dengan sisa 11.
• Karena 11 termasuk dari bilangan di antara 10 dan 15, maka 11 kita ganti dengan karakter huruf.
• Untuk 11 karakter hurufnya adalah B dan kita catat B sebagai sisa.
• Lanjut lagi 1 bagi 16, karena dapat hasil yang sudah menyentuh angka 0 maka pembagian selesai.
• Karena ada sisa, maka sisanya kita catat dengan nilai 1.

Berikut ini adalah tahapan pembagian yang dimulai dari kiri ke kanan.

Proses perhitungan modulus telah selesai, kita kumpulkan setiap nilai dari sisa dari kanan ke kiri.

Maka hasil akhir yang diperoleh adalah 435₁₀ = 1B3₁₆.

 

Rangkuman

---

Jadi desimal yang kita bahas padi artikel ini bukanlah bilangan di belakang koma, namun sebuah sistem bilangan.

Sistem bilangan desimal adalah sistem bilangan yang umum manusia gunakan sehari-hari.

Angka-angka yang kita pelajari saat masih kecil merupakan karakter yang sama di dalam sistem bilangan ini.

Desimal sendiri berbasis 10, jadi ada 10 karakter yang bisa kita pakai, yaitu karakter 0 sampai 9.

Sama seperti biner dan sistem bilangan lainnya, kita bisa mengkonversi nilai desimal ke dalam sistem bilangan yang lain.

Sekian untuk artikel ini, terima kasih.